The magic of XOR

XOR is an interesting operation and stands for 'exclusive OR'.  In this post, I will cover few problems which can be solved by using XOR.

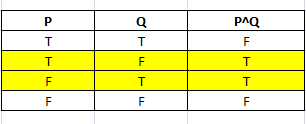
Truth Table:

P ^ Q == (~P & Q) | (P & ~Q)

Problem 1:  Find number occurring odd no.of times

We can solve this problem by exploiting below mentioned XOR property.

p1^p2^p3^...^pn = true if no. of variables with the value true is ODD

p1^p2^p3^...^pn = false if no. of variables with the value true is EVEN

(This property doesn't hold true for variables with false value)

Problem 2: Find missing number in a range with out duplicates

1) Find XOR value of all numbers in the range

2) Find XOR value of all numbers in the array

3) XOR above values to know missing number

Problem 3: Swapping two numbers with out taking help of temp variable

Let's say we have to swap values of X and Y.

// X = A ,Y = B

// X = A ^ B, Y=B

X =  X ^ Y 

//Y = A^B ^ B -> A

Y =  X ^ Y

//A^B^A -> B

X = X ^ Y

X = B,Y=A

More about XOR on 

http://stackoverflow.com/questions/6398427/what-does-bitwise-xor-exclusive-or-mean

Hope you find this post useful.

Happy Learning

Given array and a number x, check for pair in arr with sum x

We can directly jump to brute force approach and end up with o(n2) complexity solution.










No. comparisons = ( n(n+1) / 2 ) - n where n is array length.

Problem with above approach are
a. Trying unnecessary combinations
    means more comparisons,add operations,time consumption etc
b. Giving interviewer one chance to reject us :)

Better approach 1:

Whenever we are dealing with arrays, following things, we need to keep in mind

1) Array sorting.
2) Input range.
3) minimum no.of comparisons/copy operations needed.
4) Usage of index pointers
5) Boundary conditions (<arr.length , >-1)

Most of the times, sorting and binary search combination solves most of the array problems for us.

Best thing about this approach is, we are avoiding unnecessary combinations by taking advantage of sorted data.

If we find, summation is less than X, then we should try adding next big number from beginning otherwise try adding next small number from ending.

This solution works in o(nlogn) sorting + o(n) time which is way better than o(n2).

Best apporach 2:

If there is no constraint on extra space, then we can try out below approach.

Note1: We should know range of input
Note2: This solution works for negative numbers as well !

Above approach does the trick in o(n) complexity with additional space.

Above approach works like a charm, while dealing with negative numbers. All we have to do is try converting all -ve numbers into positive ones.

     int[] arr = new int[]{1,4,45,-6,10,-8};
     int x = 2

Steps:
a) Find least minimum number and it's absolute value: |-8| = 8
b) Add 8 to all input values: {9,12,53,2,18,0}
c) Add 8 + 8 to x: 16 +2 = 8

10 + (-8) = 2
(10 + 8) + -8 = 10;
18+ -8+8 = 10+8
18 = 18

Hope you find this post useful.

Happy learning :)